Introduction to Spectral Graph Theory: Courant-Fischer Theorem

December 19, 2020December 19, 2020Themistoklis Haris

The following theorem gives a characterization of the eigenvalues of a symmetric matrix according to the Rayleigh quotient: the eigenvalues are the solution of a particular optimization problem

The Courant-Fischer Theorem

Let $M$ be a symmetric matrix with eigenvalues $\mu_1 \geq \mu_2 \geq \cdots \geq \mu_n$ . Then:

$\mu_k = \max\limits_{\substack{S\subset \mathbb{R}^n \\ dim(S) = k}} \min\limits_{\substack{x\in S \\ x\neq 0}} \frac{x^T M x}{x^T x}$ .

Proof

Step 1: Let $y_1, . . . , y_n$ be an orthonormal eigenbasis of $M$ , where $y_i$ belongs to the eigenspace of $\mu_i$ . Then we can write $x = \sum\limits_{i=1}^n c_i y_i$ , where $c_i = \langle y_i, x \rangle$ .
Step 2: We have that: $x^T M x = x^T M \left(\sum\limits_{i=1}^n c_i y_i\right) = x^T \left[\sum\limits_{i=1}^n c_i (M y_i) \right] = x^T \left (\sum\limits_{i=1}^n c_i \mu_i y_i\right) = \sum\limits_{i=1}^n c_i^2 \mu_i$ , as our basis is orthonormal.

Step 3: We prove that for some subspace $S$ of dimension $k$ we have that

$\min\limits_{\substack{x\in S \\ x\neq 0}} \frac{x^T M x}{x^T x} \geq \mu_k$ .

If we let $S = span(y_1, . . . , y_k)$ , then $x = \sum\limits_{i=1}^k c_i y_i$ and using our step 2, we get:

$\frac{x^T M x}{x^T x} = \frac{\sum\limits_{i=1}^k c_i^2 \mu_i}{\sum\limits_{i=1}^k c_i^2} \geq \frac{\sum\limits_{i=1}^k c_i^2 \mu_k}{\sum\limits_{i=1}^k c_i^2} = \mu_k$

Step 4: We prove that for all subspaces $S$ of dimension $k$ it is true that .

$\min\limits_{\substack{x\in S \\ x\neq 0}} \frac{x^T M x}{x^T x} \leq \mu_k$

We consider $T = span (y_k, . . . , y_n)$ of dimension $n-k+1$ . $S\cap T$ has dimension at least 1. So:

$\min\limits_{\substack{x\in S \\ x\neq 0}} \frac{x^T M x}{x^T x} \leq \min\limits_{\substack{x\in S\cap T\\ x\neq 0}} \frac{x^T M x}{x^T x} \leq \max\limits_{\substack{x\in T\\ x\neq 0}} \frac{x^T M x}{x^T x}$

Writing $x = \sum\limits_{i=1}^{k} c_i y_i$ for any $x \in T$ , we get that:

$\frac{x^T M x}{x^T x} = \frac{\sum\limits_{i=k}^n c_i^2 \mu_i}{\sum\limits_{i=k}^n c_i^2} \leq\frac{\sum\limits_{i=k}^n c_i^2 \mu_k}{\sum\limits_{i=k}^n c_i^2} = \mu_k$

From steps 3 and 4, our proof concludes.

Linear Algebra Essentials: PART 1

December 18, 2020December 19, 2020Themistoklis Haris

1. An introduction

Theorem 1

Let $V$ be an inner product space over $F$ and let $g\,:\,V\rightarrow F$ be a linear transformation. Then there exists a unique vector $y \in V$ such that $g(x) = \langle x,y \rangle$ for all $x \in V$ .

Definition

Let $T$ be a linear operator on an inner product space $V$ . The unique linear operator $T^*$ which is such that $\langle T(x), y\rangle = \langle x, T^*(y)\rangle$ is called the adjoint of $T$ .

Theorem 2

The adjoint of any linear operator exists.

Theorem 3

Let $V$ be a finite-dimensional inner product space, and let $\beta$ be an orthonormal basis for $V$ . Then $[T^*]_\beta = [T]_\beta^*$ .

Corollary: $L_{A^*} = (L_A)^*$

2. Proofs to the Theorems

PROOF OF THEOREM 1 (Every linear operator is an inner product operator)

Let $\beta=\{u_1,u_2, . . . ,u_n\}$ be a base for $V$ . Let A

$y = \sum\limits_{i=1}^n \overline{g(u_i)}u_i$ .

Then let $h(x) := \langle x,y\rangle$ . For $i \in [n]$ we have: $h(u_i) = \langle u_i, \sum\limits_{j=1}^n \overline{g(u_j)}u_j \rangle = \sum\limits_{j=1}^n g(u_j) \langle u_i, u_j \rangle = g(u_i)$ . Since $h$ and $g$ agree on every element of $\beta$ , they are equal linear operators. The uniqueness of $y$ follows easily through a contradiction argument.

PROOF OF THEOREM 2 (existence and uniqueness of the adjoint linear operator)

Let $y \in V$ . Define $g(x) = \langle T(x), y \rangle$ . It is easy to see that $g$ is linear. So, by Theorem 1, there exists a $y^* \in V$ such that $g(x) = \langle x, y^* \rangle$ . Defining $T^*(y) = y^*$ gives us the adjoint. Linearity and uniqueness follow easily.

PROOF OF THEOREM 3 (Adjoint representative is representative of conjugate transpose)

If $\beta=\{u_1,u_2, . . . ,u_n\}$ , then $([T^*]_\beta)_ij = \langle T^*(u_j), u_i \rangle = \overline{\langle T(u_i), u_j \rangle} = [T_\beta]^*$ .

Riemann’s Rearrangement Theorem

August 11, 2019September 7, 2020Themistoklis Haris

This post will be devoted to a very special and surprising result given by the great Bernhard Riemann on the topic of the convergence of infinite series.

The theorem states:

Let $\{a_n\}_{n=1}^{\infty}$ be a sequence of real numbers so that $\sum\limits_{n=1}^{\infty} a_n$ is conditionally convergent (it converges but not absolutely). Then if we let $M\in\mathbb{R}\cup\{\infty,-\infty\}$ , there exists a permutation $\sigma$ of $\{a_n\}$ such that $\sum\limits_{n=1}^{\infty} a_{\sigma(n)} = M$

Let’s let that result sink in first through a classic example. Consider the series $1 - \frac{1}{2} + \frac{1}{3} - \cdots = \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}$ . We know this series converges to $ln(2)$ , through Taylor’s series but the series $\sum\limits_{n=1}^{\infty}\frac{1}{n}$ is the harmonic series and diverges. So our series is conditionally convergent. But observe that we can rearrange the terms of the infinite sum so that the series converges to the half of itself:

$\left(1-\frac{1}{2}-\frac{1}{4}\right) + \left(\frac{1}{3}-\frac{1}{6} - \frac{1}{8}\right) + \left(\frac{1}{5} - \frac{1}{10} - \frac{1}{12}\right) + \cdots = \sum\limits_{n=1}^{\infty}\left(\frac{1}{2n-1}-\frac{1}{4n-2} - \frac{1}{4n}\right) = \sum\limits_{n=1}^{\infty}\frac{1}{4k(2k-1)} = \frac{1}{2}ln(2)$

This is very weird. The same numbers added up in different order up to infinity, lead to a different sum. So addition works in strange ways when we take limits to infinity. We already sort of knew that but this theorem showcases it to an extent I couldn’t imagine before. And not only can we get half our sum by rearranging the terms, but we can get all possible numbers, by rearranging the terms in some way. We can even get $\pm \infty$ .

We should prove this important theorem. In fact we shall prove a stronger statement: that if $-\infty \leq a \leq b \leq \infty$ , there exists a rearrangement $\sigma$ of $\{a\}_{n=1}^{\infty}$ such that

$\liminf_{n\rightarrow\infty}s_n'= a$ and $\limsup_{n\rightarrow \infty}s_n' = b$ ,

where $s_n'$ is the sequence of partial sums of the rearranged sequence.

We get our result immediately if $a=b$ . In case there is confusion about the $\limsup$ and $\liminf$ notation, recall that these signify the limit superior and limit inferior of a sequence, which are limiting bounds on a sequence (more info here).

First, define the following sequences: $p_n = \frac{|a_n| + a_n}{2}$ and $q_n = \frac{|a_n|-a_n}{2}$ . So $p$ consists of all the positive terms in $a$ and of 0s in the place of the negative terms and $q$ is the opposite.

FACT: $p$ and $q$ diverge.

This isn’t very hard to see. If they both converged then $\sum|a_n|$ would have to converge and if one converged and one diverged then $\sum a_n$ would converge (check this!)

Now consider the sequences $P_n, Q_n$ of positive terms and of the absolute values of the negative terms in order in $\sum a_n$ . P and Q differ from p and q only in the placement of 0s in between of the latters’ terms, so both P and Q diverge.

IDEA / GOAL: Construct sequences $\{m_n\}, \{k_n\}$ such that the series

$P_1 + \cdots P_{m_1} - Q_1 -\cdots - Q_{k_1} + \\[1mm] P_{m_1+1} + \cdots + P_{m_2} - Q_{k_1+1} - \cdots - Q_{k_2} + \cdots$

,which is obviously a rearrangement of $\sum a_n$ satisfy our theorem’s target.

How to do this? First choose sequences $\alpha_n \rightarrow a, \beta_n \rightarrow b$ so that $\beta_1 > 0$ and $\alpha_n < \beta_n$ . Then let $m_n$ and $k_n$ be the smallest integers such that

$x_n = \sum\limits_{i=0}^{m_n}P_i - \sum\limits_{i=0}^{k_{n-1}} Q_i > \beta_n$ and $y_n = \sum\limits_{i=0}^{m_n}P_i - \sum\limits_{i=0}^{k_n} Q_i < \alpha_n$ (let $k_0 = -1$ )

We can always find such integers because $P, Q$ diverge.

Since $m_n$ and $k_n$ are the smallest integers with this property, we have that $|x_n - \beta_n| \leq P_{m_n}$ and $|y_n - \alpha_n| \leq Q_{k_n}$ so that $x_n \rightarrow a$ and $y_n \rightarrow b$ .

Finally, it is clear that no subsequential limit of our rearranged series can converge to something larger than b or smaller than a and so our proof is complete.

Proof adapted from the book “Principles of Mathematical Analysis”, by Walter Rudin.

Bertrand’s Postulate – a BOOK proof

July 9, 2019September 7, 2020Themistoklis Haris

I really enjoyed reading Erdos’s proof of Bertrand’s postulate in “Proofs from THE BOOK”, so I shall attempt writing out here in order to make sure I understand it properly.

Bertrand’s Postulate

For any $n>0$ , there exists a prime number $p$ such that

$\boxed{n < p \leq 2n}$

Proof

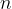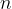The main idea of the proof is estimating the binomial coefficient $2n\choose n$ by using the prime numbers in its factorization. If it were the case that no prime existed between $n$ and $2n$ , then we will see that our bound will enforce $n$ to be small. How small we shall see. But we will end up proving that the statement holds for $n<k$ for some $k>0$ , using a certain clever trick. To get there though, we first have to work on some bounding.

PART 1: THE “BIG” PRIMES IN $\,2n \choose n$

First, let $p\geq 2$ be a prime. By Legendre’s formula, we know that the largest power of $p$ dividing $2n\choose n$ is given by:

$v_p\left(2n\choose n\right) = v_p\left(\frac{(2n)!}{(n!)^2}\right) = \sum\limits_{k\geq 1}\left(\left\lfloor\frac{2n}{p^k}\right\rfloor-2\left\lfloor\frac{n}{p^k}\right\rfloor\right)$

Each summand is at most one since,

$\left\lfloor\frac{2n}{p^k}\right\rfloor-2\left\lfloor\frac{n}{p^k}\right\rfloor < \frac{2n}{p^k}-2\left(\frac{n}{p^k}-1\right) = 2$

Furthermore, if $p^k > 2n$ , then the summand is equal to zero. Thus,

$v_p\left(2n\choose n\right) \leq \max\,\{r\colon p^r \leq 2n\}$

This inequality yields some very useful facts:

The largest power of $p$ that divides $2n\choose n$ is not larger than $2n$ .
Primes $p > \sqrt{2n}$ appear at most once in $2n \choose n$ .

Now, primes $p$ such that $\,\frac{2}{3}n < p \leq n$ cannot divide $2n\choose n$ . $3p > 2n$ so $2p > 2n-p$ . And $p \leq n$ , so $2p > n$ . Thus, in $\frac{(2n)!}{(n!)^2}$ , we have $p$ appearing only once in the numerator and twice in the denominator.

PART 2: BOUNDING $\, 2n\choose n$

First some background on the binomial coefficients. We know the following properties:

$\sum\limits_{k=0}^{n} {n\choose k} = 2^n$
${n \choose k} = {n \choose n-k}$
${n \choose k} = \frac{n-k+1}{k}{n\choose k-1}$ . Using this and (2) we can prove that:
$1 = {n\choose 0} < {n \choose 1} <\cdots< {n \choose \lfloor n/2 \rfloor} = {n \choose \lceil n/2 \rceil} >\cdots> {n \choose n-1} > {n \choose n} = 1$ (unimodal sequence)

From (1) we know that for all 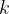$k$ it is true that ${n \choose k} \leq 2^n$ . From (4) we know that ${n \choose \lfloor n/2 \rfloor} \geq \frac{2^n}{n}$ , since the largest element in a sequence is greater than or equal to the average of the sequence. Now we can infer that

$\boxed{{2n \choose n} \geq \frac{4^n}{2n}}$

So we have now (CRUX MOVE):

$\boxed{\frac{4^n}{2n} \leq {2n \choose n} \leq \prod\limits_{p\leq \sqrt{2n}}{2n}\cdot\prod\limits_{\sqrt{2n} < p \leq \frac{2}{3}n}p\cdot\prod\limits_{n<p\leq 2n}p}$

To make sure you understand why this holds, be able to answer the following:

Why do we take primes only up to $2n$ ?
Why do we not take any primes between $\frac{2}{3}n$ and $n$ ?
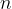Why is the exponent of each prime 1?

Now we have:

$4^n \leq (2n)^{1+\sqrt{2n}}\cdot \prod\limits_{\sqrt{2n}<p\leq\frac{2}{3}n}p\cdot\prod\limits_{n<p\leq 2n}p$

Let’s assume, for the sake of contradiction, that there are no primes between 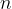$n$ and $2n$ . Then the inequality above becomes:

$4^n \leq (2n)^{1+\sqrt{2n}}\cdot \prod\limits_{\sqrt{2n}<p\leq\frac{2}{3}n}p$

We shall show that for this to hold, 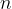$n$ must be small enough that we will actually be able to prove Bertrand’s postulate for such $n$ .

First we need the following lemma:

LEMMA

For all reals $x\geq 2$ , we have that

$\boxed{\prod\limits_{p\leq x}p \leq 4^{x-1}}$

Proof

Let $q$ be the largest prime with $q\leq x$ . Then $\prod\limits_{p\leq x}p = \prod\limits_{p \leq q}p$ and $4^{q-1} \leq 4^{x-1}$ , so it suffices to prove our statement for $x = q$ prime. For $q=2$ the result is trivial and so we consider odd primes $q = 2m+1$ .

Then we inductively compute:

$\prod\limits_{p \leq 2m+1}p = \prod\limits_{p \leq m+1}p \cdot \prod\limits_{m+1 < p \leq 2m+1}p \leq 4^m{{2m+1}\choose m} \leq 4^m 2^{2m} = 4^{2m}$

There are a few parts to this computation:

$\prod\limits_{p \leq m+1}p \leq 4^m$ holds by induction.
$\prod\limits_{m+1 < p \leq 2m+1}p \leq {{2m+1}\choose m}$ comes from the observation that ${{2m+1}\choose m} = \frac{(2m+1)!}{m!(m+1)!}$ is an integer, where the primes we consider are all factors of the denominator but not of the numerator.
Finally, ${{2m+1}\choose m} \leq 2^{2m}$ form the properties (1) and (2) of the binomial coefficient presented above.

PART 3: GETTING THE CONTRADICTION

The last Lemma we proved as well as the inequality above yield that:

$4^n \leq (2n)^{1+\sqrt{2n}}4^{\frac{2}{3}n} \Leftrightarrow 4^{\frac{1}{3}n} \leq (2n)^{1+\sqrt{2n}}$

With some clever algebra we can see that this fails to hold for large 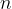$n$ . First, we know by induction that if $a\geq 2$ , then $a+1 < 2^a$ . So:

$2n = \left(\sqrt[6]{2n}\right)^6 < \left(\lfloor\sqrt[6]{2n}\rfloor + 1\right)^6 < 2^{6\lfloor\sqrt[6]{2n}\rfloor} \leq 2^{6\sqrt[6]{2n}}$

Now:

$2^{2n} \leq (2n)^{3\left(1+\sqrt{2n}\right)} < 2^{\sqrt[6]{2n}\left(18+18\sqrt{2n}\right)} \overset{n\geq 50}{<} 2^{20\sqrt[6]{2n}\sqrt{2n}}= 2^{20(2n)^{2/3}}$

So we get $(2n)^{1/3} < 20$ and thus $n < 4000$ . This is a contradiction because we can easily show Bertrand’s postulate to hold for $n < 4000$ . An impressive trick to establish this right away is due to Landau:

It suffices to check that the sequence

2, 3, 5, 7, 13, 23, 43, 83, 163, 317, 631, 1259, 2503, 4001

consists of prime number where each is smaller than twice the previous one. Thus every interval $\{y\colon n < y \leq 2n\}$ with $n \leq 4000$ contains one of these 14 primes and our proof concludes.

On the infinitude of primes – Erdős’s proof

July 5, 2019September 7, 2020Themistoklis Haris

In the book “Proofs from THE BOOK”, there are 6 proofs on the infinitude of primes. All of them are very elegant and beautiful but I really liked the reasoning behind the following one, coined by Paul Erdos.

We shall prove that the series

$\sum\limits_{p \in \mathbb{P}}\frac{1}{p}$

diverges. That would imply that the set of prime numbers in infinite because otherwise their sum would converge.

Let $\{p_i\}_{i \in \mathbb{N}}$ be the sequence of primes numbers written in increasing order.

Assume that the series above converges. Then, there must exist some number $k$ such that

$\sum\limits_{i \geq k+1}\frac{1}{p_i} < \frac{1}{2}$

Call the primes $p_i$ for $1 \leq i \leq k$ the small primes and the rest the big primes.

For any natural number $N$ , it must then hold that

$\boxed{\sum\limits_{i \geq k+1}\frac{N}{p_i} < \frac{N}{2}}$

Now, let $N_b$ be the number of positive integers $n \leq N$ which are divisible by at least one big prime and let $N_s$ be the number of positive integers less than or equal to $N$ whose prime divisors are all small primes.

We will show that $N_b+N_s < N$ , thus arriving at a contradiction (it should be $N_b+N_s = N$ .

First, note that $\lfloor\frac{N}{p_i}\rfloor$ counts the number of positive integers less than or equal to $N$ that are multiples of $p_i$ .

We have that

$N_b \leq \sum\limits_{i \geq k+1}\lfloor\frac{N}{p_i}\rfloor < \frac{N}{2}$

and this equation allows us to estimate $N_b$ . For $N_s$ , let $n \leq N$ be a positive integer whose prime divisors are all small primes. Let $n = a_n b_n^2$ , where $a_n$ is not a square of an integer. Since $a_n$ cannot contain the same small prime number twice in its prime factor decomposition, it can take exactly $2^k$ values. And given that $b_n \leq \sqrt{N}$ , we have that