Month: October 2019

A weak lower bound on the Communication Complexity of the Disjointness Function

Themistoklis Haris

Any private-coin randomized protocol \pi that computes DISJ_n with an error probability of at most \epsilon cannot use less than some multiple of \sqrt{n} bits in the worst case.

Invoke Newman’s Theorem 

R^{priv}_{\epsilon}(DISJ_n) = R^{pub}_{\epsilon-\delta} (DISJ_n) + O(\log n + \log \delta^{-1}).

Since \sqrt{n} \gg \log n asymptotically, it suffices to show that

R^{pub}_{\epsilon} (DISJ_n) = \Omega (\sqrt{n}), for \epsilon \leq \frac{1}{3}

Now recall Yao’s Lemma:

R^{pub}_{\epsilon} (DISJ_n) \geq \max_{\mu}\{D^{\mu}_{\epsilon}(DISJ_n)

which allows us to reduce the problem to coming up with a probability distribution \mu over X \times Y = \{0,1\}^n\times\{0,1\}^n such that any deterministic protocol which errs with probability of at most \epsilon on any input according to \mu communicates at least some multiple of \sqrt{n} bits in the worst case.

One initial thought worth investigating is what happens when if \mu = uniform. Suppose Alice and Bob both choose any subset of [n] uniformly. Then the probability that they choose disjoint subsets is \left(\frac{3}{4}\right)^n, which goes to 0 as n grows large. So a protocol that just outputs 0 (they are NOT disjoint) can be made to have an arbitrarily small error asymptotically, which means that we only get an \Omega(1) bound by using the uniform distribution. We are not satisfied.

Instead, consider the following product distribution: Alice and Bob cannot possibly pick a subset of [n] whose size is different that \sqrt{n} and they pick subsets of size \sqrt{n} with uniform distribution. So \mu = \lambda \times \rho, where:

\lambda(X) = \rho(X) = \left\{ \begin{array}{ll} \!\! \frac{1}{\binom{n}{\sqrt{n}}}, &|X| = \sqrt{n}\\ \!\! 0, &\text{otherwise}\end{array}\right.

In this case, the probability that Alice and Bob choose disjoint subsets is:

\left(\frac{n-\sqrt{n}}{n}\right)^{\sqrt{n}} \approx \frac{1}{e}

We will show that any deterministic protocol that, under \mu, errs with a probability of at most \epsilon in calculating DISJ_n, uses at least some factor of \sqrt{n} in the worst case.

The intuition is as follows: Let \pi be the (\epsilon-\mu) protocol with the minimum communication complexity. \pi partitions X\times Y into rectangles, corresponding to its leaves. For each rectangle, \pi answers in the same way in the question of whether the two input subsets are disjoint or not.

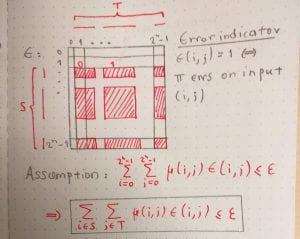
However, some of these rectangles may be corrupted. In other words, the protocol may output that the input sets are disjoint, when in fact they are not. Let’s look at 1-rectangles. That is, rectangles in which the protocol answers YES, they are disjoint (1). We know that \pi errs with a probability of at most \epsilon. Therefore, all of its rectangles have small corruption. Specifically, if R = S\times T is an 1-rectangle, then

Pr_{\mu}\{DISJ(x,y)=0\,|,\, (x,y) \in R\} \leq \epsilon

The figure below illustrates why that is.


We show that exactly because the rectangles of \pi cannot be too corrupted, they have to be small in size (their measure according to \mu is small). This will imply that there are many of them and so we will have a lower bound to the communication complexity.

To elaborate further on this, let A be the maximum \mu-measure of any 1-rectangle of \pi. If we suppose for the purposes of contradiction that CC(\pi) \leq \alpha\sqrt{n} for some \alpha, then the number of 1-rectangles is bounded above by the number of leaves of \pi, which in turn is bounded above by 2^{\alpha\sqrt{n}}.

1 = \sum\limits_{R}\mu(R) \leq 2^{\alpha\sqrt{n}}A

And so A \geq 2^{-\alpha\sqrt{N}}. In other words, if the communication complexity of \pi is small, there must be a big 1-rectangle. And that rectangle has low corruption. We prove that this is impossible, acquiring a contradiction.

We prove the following Lemma (I):

“If R=S\times T is a 1-rectangle of \pi,

then either |T| or |S| has to be at most 2^{-c\sqrt{n}}\binom{n}{\sqrt{n}} for some constant c.”

After establishing this, if we let R = S \times T be a 1-rectangle of \pi and assume WLOG that |T| \leq |S|, then |T| \leq 2^{-c\sqrt{n}}\binom{n}{\sqrt{n}} by Lemma I, and so

\mu(R) = \sum\limits_{s\in S, t\in T} \mu(s,t) = \left(\sum\limits_{s\in S}\lambda(s)\right)\left(\sum\limits_{t\in T} \rho(t)\right) \leq 1\cdot \frac{|T|}{\binom{n}{\sqrt{n}}} \leq 2^{-c\sqrt{n}},

which implies that every 1-rectangle R must be small, thus giving us our contradiction.

Heading over to the proof of Lemma I, we first two simplifying assumptions:

  • S is large (we will formalize this below but if S were small then our lemma holds vacuously).
  • All the subsets of [n] lying in S and T have size \sqrt{n}. There is 0 probability of getting subsets of size \neq \sqrt{n} as inputs, so Alice and Bob can modify \pi to immediately reject such input cases so that we don’t have to worry about its behavior on them.

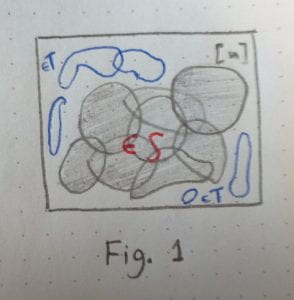
Intuition: If S is large, then its sets must span a large fraction of [n]. There cannot exist too many sets disjoint with the sets of S then. So T is small. This is illustrated in the figure below:

We shall start by proving that the span of the elements of S has to be big. This is the following Lemma, which could be stated without any relation to our communication complexity investigations:

LEMMA II: Let Q be a collection of subsets of size \sqrt{n} of [n]. Then there exists some c'>0 such that if |Q| > \frac{1}{2} 2^{-c' \sqrt{n}} \binom{n}{\sqrt{n}}, then for k = \frac{\sqrt{n}}{3}, there exist sets x_1, x_2, . . ., x_k \in Q such that \forall i=1,2, . . ., k it holds that

\left|x_i \cap \bigcup\limits_{j<i}x_j \right| < \frac{\sqrt{n}}{2}

Proof

We show that if we pick any l < \frac{\sqrt{n}}{3} sets x_1, x_2, . . ., x_l \in Q, we can find another set x^{*} \in Q that shares less that \frac{\sqrt{n}}{2} elements with the l sets we picked.

In other words:

\left|x^{*} \cap \bigcup\limits_{i\leq l} x_i\right| < \frac{\sqrt{n}}{2}

This gives us an incremental procedure of finding the collection x_1, x_2, . . ., x_k: Every new set we add has less than \frac{\sqrt{n}}{2} common elements with all the previous sets chosen and this is exactly what we want to prove. This is shown in the figure below:

|Z| = \left|\bigcup\limits_{i\leq l} x_i\right| \leq \sqrt{n}\cdot\frac{\sqrt{n}}{3} = \frac{n}{3} \Rightarrow |\{x \in Q\,:\, |x\cap Z| \geq \frac{\sqrt{n}}{2}| \leq

\leq \sum\limits_{i=\sqrt{n}/2}^{\sqrt{n}}\binom{n/3}{i}\binom{2n/3}{\sqrt{n}-i} \leq n\binom{n/3}{\sqrt{n}/2}\binom{2n/3}{\sqrt{n}/2} < 2^{-1-c'\sqrt{n}}\binom{n}{\sqrt{n}} < |Q|

for large enough n, where the constant c'>0 is obtained through Stirling’s approximation \log_2 (n!) = n\log_2 n - n\log_2 e + O(log_2 n). This concludes the proof of Lemma (II) because we have found that there must exist some x^{*} \in Q such that |x^{*} \cap Z| < \sqrt{n}/2.

Note that this Lemma implies that Q spans a large portion of U. Since each one of the x_i-s adds at least another \sqrt{n}/2 new elements, we have that |\cup_{x \in Q}| \geq \frac{\sqrt{n}}{3}\cdot \frac{\sqrt{n}}{2} = \frac{n}{6}, meaning that Q spans at least one sixth of U, which is a good fraction for our purposes.

Let’s now see exactly how S having a large span forces T to be small. The main idea lies in the fact that R has low corruption, so we seek sets that are disjoint with most sets in S and that number is bounded above because of the large span property.

Let S' to be the set of elements in S which are such that they intersect with a fraction of at most 2\epsilon of the sets of T. We must have |S'| \geq \frac{|S|}{2}, as if that wasn’t the case, there would be more than \epsilon|S||T|\, 0s of DISJ_n in R and, because both S and T consist of rectangles of size \sqrt{n} which we uniformly sample, that would violate our low-corruption hypothesis.

Applying Lemma II to S', we get that there exists some constant c'>0 such that if |S'| > 2^{-1-c'\sqrt{n}}\binom{n}{\sqrt{n}} – implying the largeness of S: |S| > 2^{-c'\sqrt{n}}\binom{n}{\sqrt{n}}) – then there exists a sub-collection x_1, x_2, . . ., x_k of S' with k = \sqrt{n}/3 whose span over U is big as we saw before.

So let’s assume that |S| > 2^{-c'\sqrt{n}}\binom{n}{\sqrt{n}} as dictated above and let us take S'' = \{x_1,x_2, . . ., x_k\} \subset S'. Now also consider the sub-collection of T consisting of sets that have an intersection with a fraction of at most 4\epsilon elements of S''. Then T' would have to contain at least half of the elements of T – |T'| \geq \frac{|T|}{2} – as otherwise there would be more than 2\epsilon|S''||T| \geq 2\epsilon |S'||T| \geq \epsilon|S||T| 0s in R, contradicting once again our low-corruption hypothesis.

It is important to conceptually notice here how the low-corruption hypothesis forces large parts of S and T to not overlap with each other too much! So we seek sets that are mostly disjoint among the two groups. And the big span of S constrains our options greatly. We show that there cannot be that many sets by bounding T' from above.

For each set y in T', there are at most 4\epsilon k sets in S'' which intersect it. So there must exist k - 4\epsilon k = (1-4\epsilon)k sets x_{i_1},x_{i_2}, . . , x_{i_{(1-4\epsilon)k}} in S'' that all don’t intersect it, which limits how many elements y can possibly have. That is we must have that y \subseteq [n] \setminus \cup_j x_{i_j} and knowing that each x_{i_j} brings in at least \sqrt{n}/2 new elements, we must have \left|[n] \setminus \cup_j x_{i_j}\right| \leq n - (1-4\epsilon)k\frac{\sqrt{n}}{2} \leq \frac{8n}{9} assuming that \epsilon \leq 0.01. That doesn’t seem like a lot: all we said is that y must be drawn from a fraction of \frac{8}{9}-ths of the universe. But it provides us with the bound we needed.

The number of possible y-s is at most:

\binom{k}{(1-4\epsilon)k}\binom{8n/9}{\sqrt{n}} = \binom{\sqrt{n}/3}{4\epsilon\sqrt{n}/3}\binom{8n/9}{\sqrt{n}} < 2^{-1-c''\sqrt{n}}\binom{n}{\sqrt{n}},

where c'' > 0 is a constant given again by Stirling’s approximation.

So |T| \leq 2|T'| < 2^{-c''\sqrt{n}}\binom{n}{\sqrt{n}}. Taking c = min(c', c'') concludes our proof.