Any private-coin randomized protocol  that computes
that computes 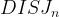 with an error probability of at most
with an error probability of at most  cannot use less than some multiple of
cannot use less than some multiple of 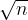 bits in the worst case.
bits in the worst case.
Invoke Newman’s Theorem
 .
.
Since  asymptotically, it suffices to show that
asymptotically, it suffices to show that
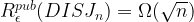 , for
, for 
Now recall Yao’s Lemma:
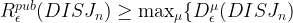
which allows us to reduce the problem to coming up with a probability distribution 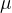 over
over  such that any deterministic protocol which errs with probability of at most
such that any deterministic protocol which errs with probability of at most  on any input according to
on any input according to 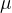 communicates at least some multiple of
communicates at least some multiple of 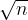 bits in the worst case.
bits in the worst case.
One initial thought worth investigating is what happens when if 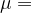 uniform. Suppose Alice and Bob both choose any subset of
uniform. Suppose Alice and Bob both choose any subset of ![[n] [n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=000000&s=1) uniformly. Then the probability that they choose disjoint subsets is
uniformly. Then the probability that they choose disjoint subsets is  , which goes to 0 as
, which goes to 0 as 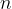 grows large. So a protocol that just outputs 0 (they are NOT disjoint) can be made to have an arbitrarily small error asymptotically, which means that we only get an
grows large. So a protocol that just outputs 0 (they are NOT disjoint) can be made to have an arbitrarily small error asymptotically, which means that we only get an  bound by using the uniform distribution. We are not satisfied.
bound by using the uniform distribution. We are not satisfied.
Instead, consider the following product distribution: Alice and Bob cannot possibly pick a subset of ![[n] [n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=000000&s=1) whose size is different that
whose size is different that 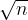 and they pick subsets of size
and they pick subsets of size 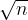 with uniform distribution. So
with uniform distribution. So  , where:
, where:

In this case, the probability that Alice and Bob choose disjoint subsets is:

We will show that any deterministic protocol that, under 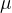 , errs with a probability of at most
, errs with a probability of at most  in calculating
in calculating 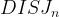 , uses at least some factor of
, uses at least some factor of 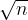 in the worst case.
in the worst case.
The intuition is as follows: Let  be the
be the 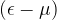 protocol with the minimum communication complexity.
protocol with the minimum communication complexity.  partitions
partitions  into rectangles, corresponding to its leaves. For each rectangle,
into rectangles, corresponding to its leaves. For each rectangle,  answers in the same way in the question of whether the two input subsets are disjoint or not.
answers in the same way in the question of whether the two input subsets are disjoint or not.
However, some of these rectangles may be corrupted. In other words, the protocol may output that the input sets are disjoint, when in fact they are not. Let’s look at 1-rectangles. That is, rectangles in which the protocol answers YES, they are disjoint (1). We know that  errs with a probability of at most
errs with a probability of at most  . Therefore, all of its rectangles have small corruption. Specifically, if
. Therefore, all of its rectangles have small corruption. Specifically, if  is an 1-rectangle, then
is an 1-rectangle, then
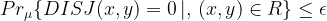
The figure below illustrates why that is.
We show that exactly because the rectangles of  cannot be too corrupted, they have to be small in size (their measure according to
cannot be too corrupted, they have to be small in size (their measure according to 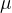 is small). This will imply that there are many of them and so we will have a lower bound to the communication complexity.
is small). This will imply that there are many of them and so we will have a lower bound to the communication complexity.
To elaborate further on this, let 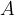 be the maximum
be the maximum 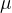 -measure of any 1-rectangle of
-measure of any 1-rectangle of  . If we suppose for the purposes of contradiction that
. If we suppose for the purposes of contradiction that  for some
for some  , then the number of 1-rectangles is bounded above by the number of leaves of
, then the number of 1-rectangles is bounded above by the number of leaves of  , which in turn is bounded above by
, which in turn is bounded above by  .
.

And so  . In other words, if the communication complexity of
. In other words, if the communication complexity of  is small, there must be a big 1-rectangle. And that rectangle has low corruption. We prove that this is impossible, acquiring a contradiction.
is small, there must be a big 1-rectangle. And that rectangle has low corruption. We prove that this is impossible, acquiring a contradiction.
We prove the following Lemma (I):
“If  is a 1-rectangle of
is a 1-rectangle of  ,
,
then either 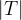 or
or 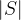 has to be at most
has to be at most  for some constant
for some constant  .”
.”
After establishing this, if we let 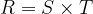 be a 1-rectangle of
be a 1-rectangle of  and assume WLOG that
and assume WLOG that  , then
, then  by Lemma I, and so
by Lemma I, and so
 ,
,
which implies that every 1-rectangle 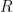 must be small, thus giving us our contradiction.
must be small, thus giving us our contradiction.
Heading over to the proof of Lemma I, we first two simplifying assumptions:
- S is large (we will formalize this below but if S were small then our lemma holds vacuously).
- All the subsets of
![[n] [n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=000000&s=0) lying in
lying in 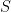 and
and  have size
have size 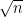 . There is 0 probability of getting subsets of size
. There is 0 probability of getting subsets of size  as inputs, so Alice and Bob can modify
as inputs, so Alice and Bob can modify 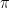 to immediately reject such input cases so that we don’t have to worry about its behavior on them.
to immediately reject such input cases so that we don’t have to worry about its behavior on them.
Intuition: If 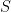 is large, then its sets must span a large fraction of
is large, then its sets must span a large fraction of ![[n] [n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=000000&s=0) . There cannot exist too many sets disjoint with the sets of
. There cannot exist too many sets disjoint with the sets of  then. So
then. So  is small. This is illustrated in the figure below:
is small. This is illustrated in the figure below:
We shall start by proving that the span of the elements of  has to be big. This is the following Lemma, which could be stated without any relation to our communication complexity investigations:
has to be big. This is the following Lemma, which could be stated without any relation to our communication complexity investigations:
LEMMA II: Let 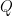 be a collection of subsets of size
be a collection of subsets of size 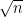 of
of ![[n] [n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=000000&s=0) . Then there exists some
. Then there exists some 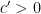 such that if
such that if  , then for
, then for 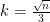 , there exist sets
, there exist sets  such that
such that  it holds that
it holds that
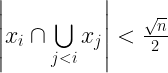
Proof
We show that if we pick any  sets
sets 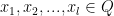 , we can find another set
, we can find another set 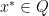 that shares less that
that shares less that  elements with the
elements with the 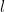 sets we picked.
sets we picked.
In other words:

This gives us an incremental procedure of finding the collection  : Every new set we add has less than
: Every new set we add has less than  common elements with all the previous sets chosen and this is exactly what we want to prove. This is shown in the figure below:
common elements with all the previous sets chosen and this is exactly what we want to prove. This is shown in the figure below:



for large enough  , where the constant
, where the constant 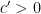 is obtained through Stirling’s approximation
is obtained through Stirling’s approximation  . This concludes the proof of Lemma (II) because we have found that there must exist some
. This concludes the proof of Lemma (II) because we have found that there must exist some 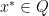 such that
such that  .
.
Note that this Lemma implies that 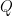 spans a large portion of
spans a large portion of 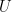 . Since each one of the
. Since each one of the  -s adds at least another
-s adds at least another  new elements, we have that
new elements, we have that  , meaning that
, meaning that 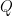 spans at least one sixth of
spans at least one sixth of 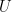 , which is a good fraction for our purposes.
, which is a good fraction for our purposes.
Let’s now see exactly how 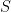 having a large span forces
having a large span forces  to be small. The main idea lies in the fact that
to be small. The main idea lies in the fact that 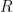 has low corruption, so we seek sets that are disjoint with most sets in
has low corruption, so we seek sets that are disjoint with most sets in 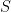 and that number is bounded above because of the large span property.
and that number is bounded above because of the large span property.
Let  to be the set of elements in
to be the set of elements in 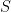 which are such that they intersect with a fraction of at most
which are such that they intersect with a fraction of at most 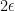 of the sets of
of the sets of  . We must have
. We must have 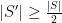 , as if that wasn’t the case, there would be more than
, as if that wasn’t the case, there would be more than 
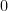 s of
s of  in
in 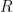 and, because both
and, because both 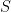 and
and  consist of rectangles of size
consist of rectangles of size 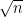 which we uniformly sample, that would violate our low-corruption hypothesis.
which we uniformly sample, that would violate our low-corruption hypothesis.
Applying Lemma II to  , we get that there exists some constant
, we get that there exists some constant 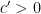 such that if
such that if 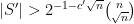 – implying the largeness of
– implying the largeness of 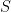 :
: 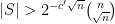 ) – then there exists a sub-collection
) – then there exists a sub-collection  of
of  with
with  whose span over
whose span over 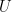 is big as we saw before.
is big as we saw before.
So let’s assume that 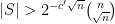 as dictated above and let us take
as dictated above and let us take  . Now also consider the sub-collection of
. Now also consider the sub-collection of  consisting of sets that have an intersection with a fraction of at most
consisting of sets that have an intersection with a fraction of at most  elements of
elements of  . Then
. Then  would have to contain at least half of the elements of
would have to contain at least half of the elements of  –
– 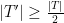 – as otherwise there would be more than
– as otherwise there would be more than 
 in
in 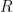 , contradicting once again our low-corruption hypothesis.
, contradicting once again our low-corruption hypothesis.
It is important to conceptually notice here how the low-corruption hypothesis forces large parts of 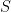 and
and  to not overlap with each other too much! So we seek sets that are mostly disjoint among the two groups. And the big span of
to not overlap with each other too much! So we seek sets that are mostly disjoint among the two groups. And the big span of 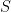 constrains our options greatly. We show that there cannot be that many sets by bounding
constrains our options greatly. We show that there cannot be that many sets by bounding  from above.
from above.
For each set  in
in  , there are at most
, there are at most 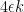 sets in
sets in  which intersect it. So there must exist
which intersect it. So there must exist 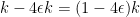 sets
sets  in
in  that all don’t intersect it, which limits how many elements
that all don’t intersect it, which limits how many elements  can possibly have. That is we must have that
can possibly have. That is we must have that ![y \subseteq [n] \setminus \cup_j x_{i_j} y \subseteq [n] \setminus \cup_j x_{i_j}](https://s0.wp.com/latex.php?latex=y+%5Csubseteq+%5Bn%5D+%5Csetminus+%5Ccup_j+x_%7Bi_j%7D&bg=ffffff&fg=000000&s=0) and knowing that each
and knowing that each  brings in at least
brings in at least  new elements, we must have
new elements, we must have ![\left|[n] \setminus \cup_j x_{i_j}\right| \leq n - (1-4\epsilon)k\frac{\sqrt{n}}{2} \leq \frac{8n}{9} \left|[n] \setminus \cup_j x_{i_j}\right| \leq n - (1-4\epsilon)k\frac{\sqrt{n}}{2} \leq \frac{8n}{9}](https://s0.wp.com/latex.php?latex=%5Cleft%7C%5Bn%5D+%5Csetminus+%5Ccup_j+x_%7Bi_j%7D%5Cright%7C+%5Cleq+n+-+%281-4%5Cepsilon%29k%5Cfrac%7B%5Csqrt%7Bn%7D%7D%7B2%7D+%5Cleq+%5Cfrac%7B8n%7D%7B9%7D&bg=ffffff&fg=000000&s=0) assuming that
assuming that  . That doesn’t seem like a lot: all we said is that
. That doesn’t seem like a lot: all we said is that  must be drawn from a fraction of
must be drawn from a fraction of 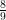 -ths of the universe. But it provides us with the bound we needed.
-ths of the universe. But it provides us with the bound we needed.
The number of possible  -s is at most:
-s is at most:
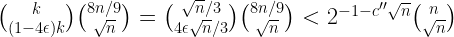 ,
,
where  is a constant given again by Stirling’s approximation.
is a constant given again by Stirling’s approximation.
So  . Taking
. Taking 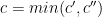 concludes our proof.
concludes our proof.
be an inner product space and
be linear operators on
. Then:
.
operator)
points
, we are trying to minimize
, with
being the line of best-fit slope and
is its offset. If
and
. We will study a general method of solving this minimization problem when
is an
matrix. This allows for fitting of general polynomials of degree
as well. We assume that
.
and
, then it is easy to see that
from the properties of the adjoint studied thus far. We also know that
by the dimension theorem, because the nullities of the two matrices are the same (this is straightforward to see). Thus, if
has rank
, then
is invertible.
, the range of
is a subspace of
. The projection of
onto
is a vector
and it is such that
for all
. To find
, let us note that
lies in
, so
for all
. In other words,
so
solves the equation
. If additionally the rank of
is
, we get that:
and suppose that the system
is consistent. Then:
to
and
.
is the only solution to
that lines in
. So, if
satisfies
, then
.
can be done by finding any solution to the system
and letting
.
, a fact which holds for all linear transformations. This fact can be easily established, so we leave it as an exercise.